画像 サイコロ 展開図 パターン 201321

立方体展開図11パターンを 全部おぼえた方がいいですか 2歳児からの考える力を伸ばす幼児教室 英才アカデミー東灘教室
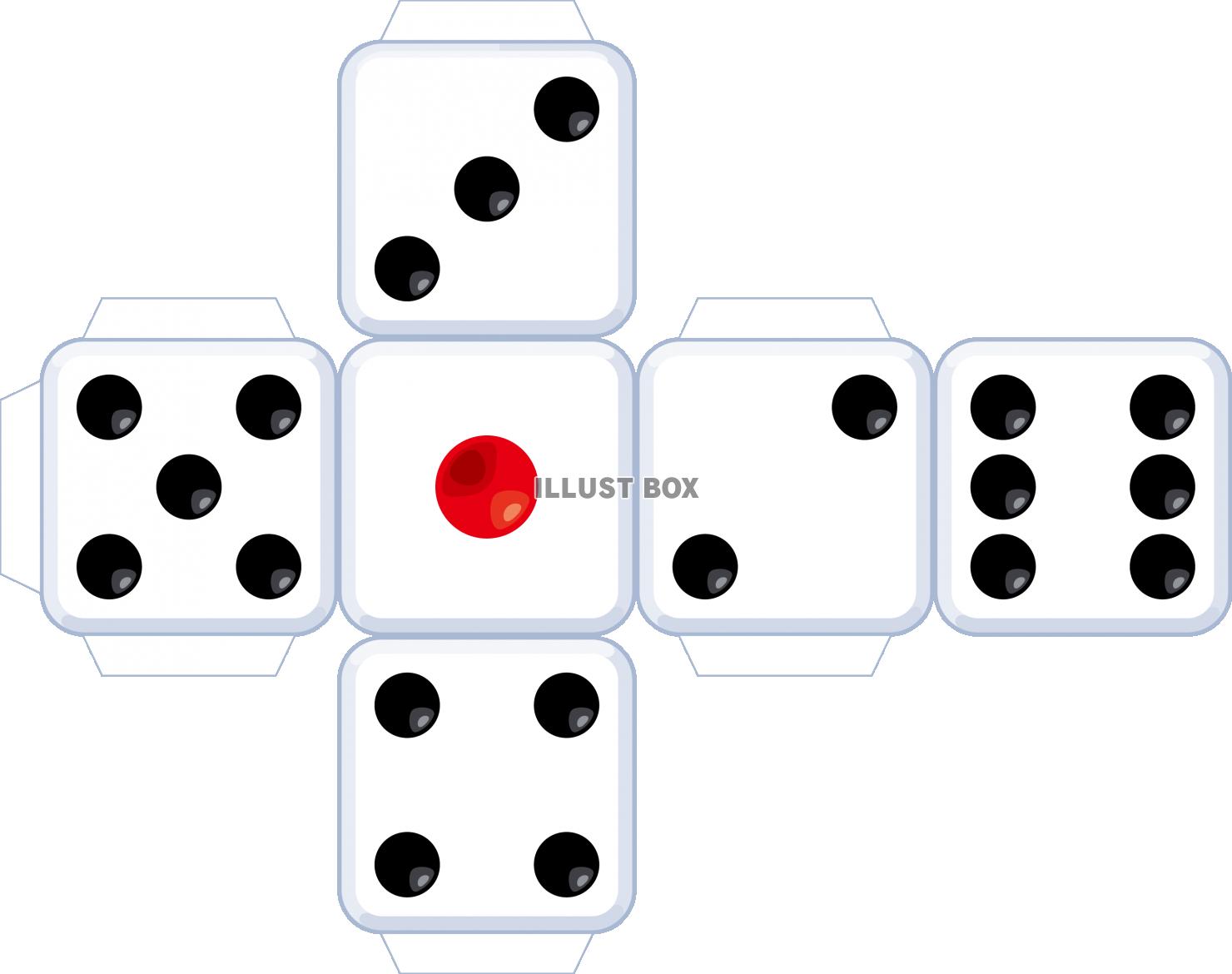
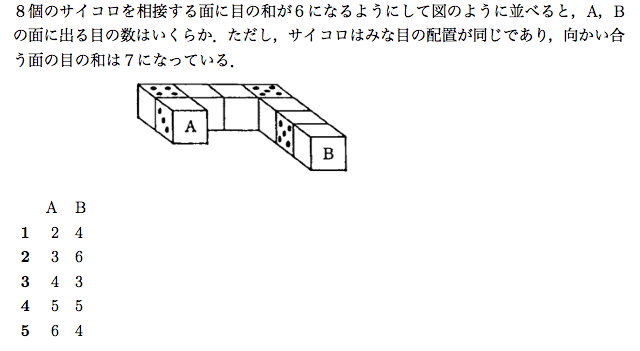
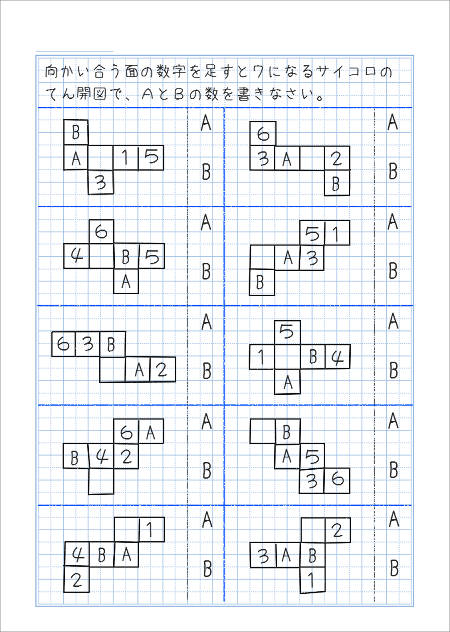
サイコロの展開図英語でダイスdice 別名賽さい形だけならば立方体とか正六面体とも 色がついているのは組み立てた時に向かい合う面 サイコロは向かい合う面の数の合計が必ず7になります これ以外にも展開図はありますが基本的にはパターンを組み替えた数基礎com 展開図のパターン全11種類が分かる方法! 展開図のパターン展開図のパターン全11種類 サイコロなど立方体の展開図をいくつか見せて、「立方体になるのはどれですか」という展開図問題は
サイコロ 展開図 パターン
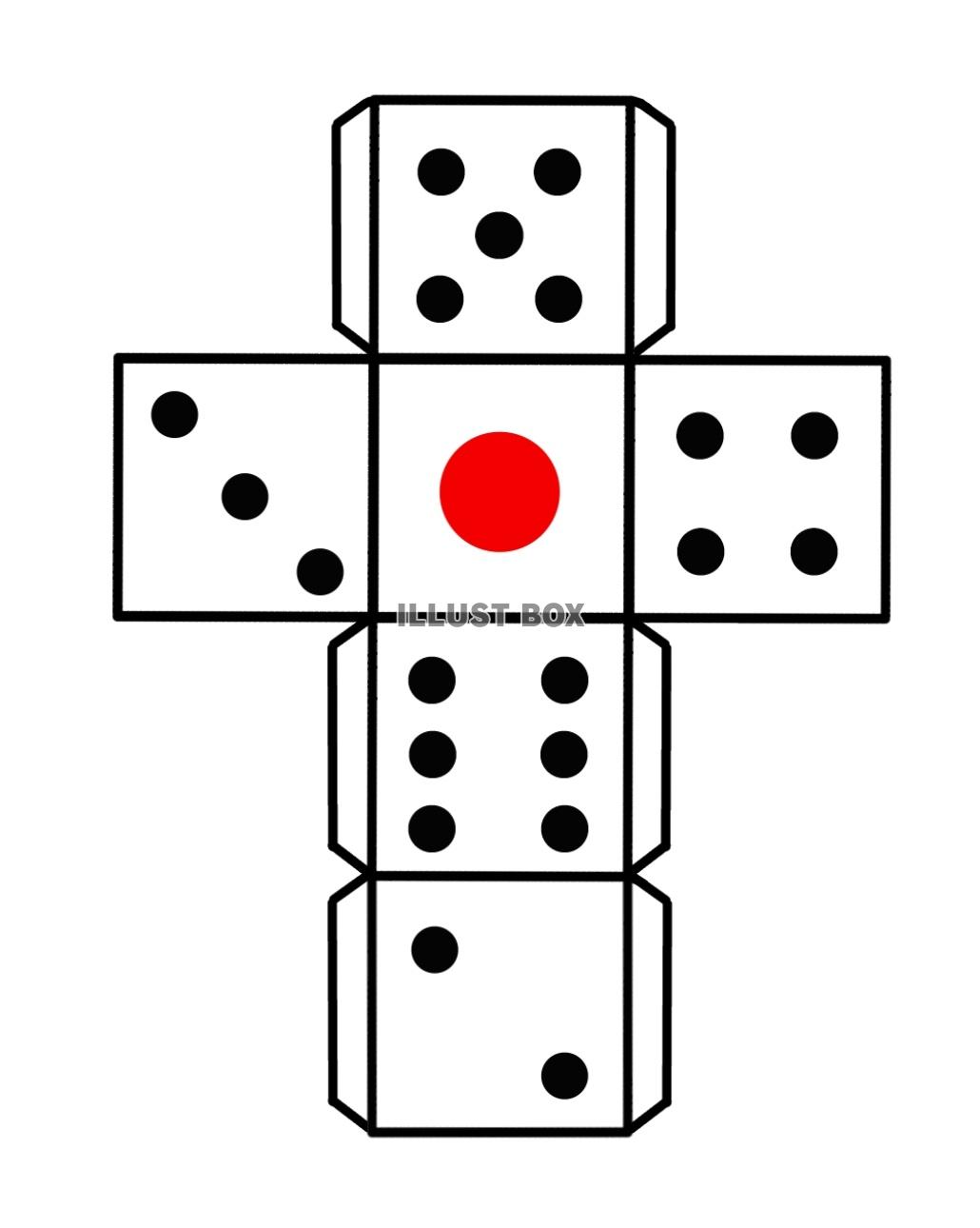
サイコロ 展開図 パターン-サイコロの展開図。英語でダイス(dice)。 別名、賽(さい)。形だけならば立方体とか正六面体とも。 色がついているのは組み立てた時に向かい合う面。 サイコロは向かい合う面の数の合計が必ず7になります。 This is "サイコロ展開図の教え方 3日目3" by TSUBASAScoa論理問題「scoaサイコロ問題」:例題2 以下はある立方体とその展開図である。この立方体を「イ→イ→イ」の方向に回転させたとき、最終的に上の面に出るものは次のどれか? (1)a (2)b (3)d (4)e (5)f
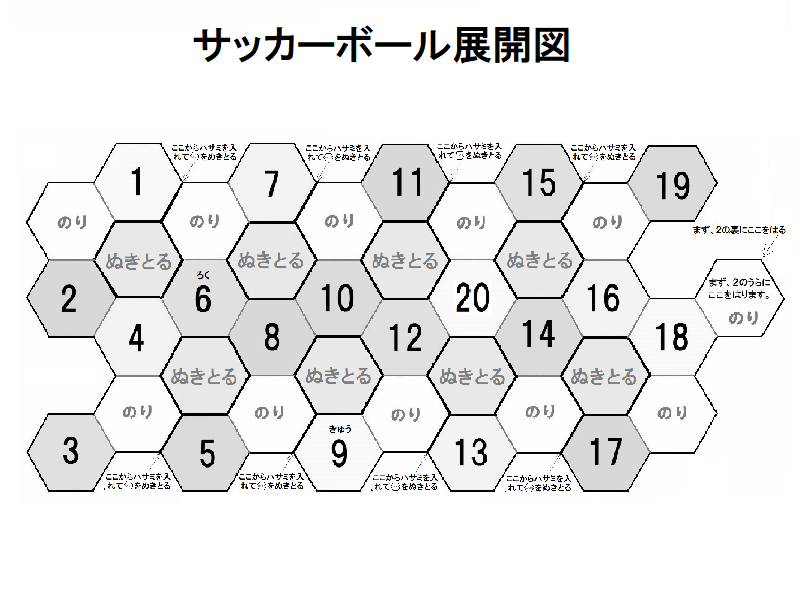
サイコロを作ろう サッカーボール 作って遊ぼう 社会に開かれた学校の応援
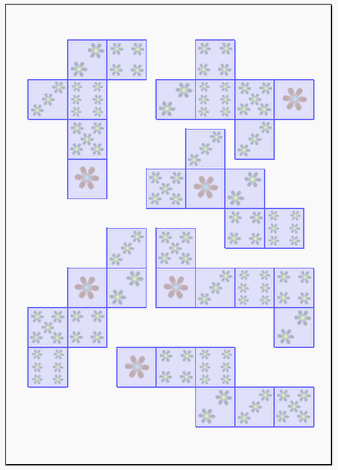
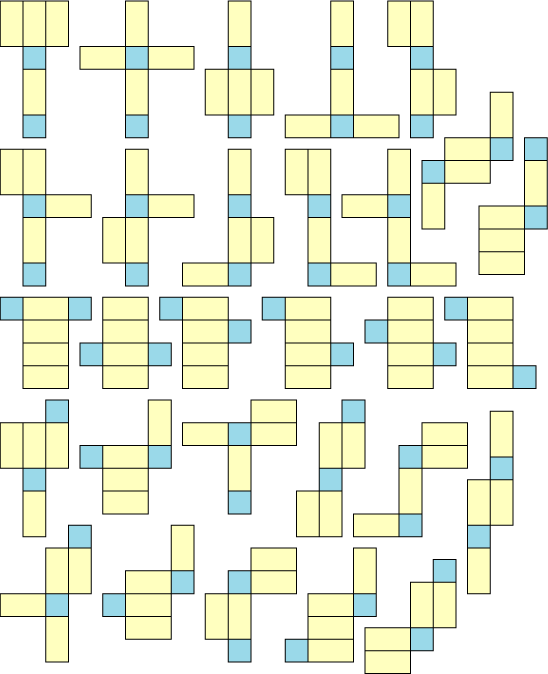
さいころの展開図一覧 前述のとおり、さいころの展開図は全部で11個 展開図を厚紙に印刷して切って組み立てるのが早く覚えるのが一番の近道です。ハサミで切り出すのも巧緻性を向上させる一つ 下記の展開図をすべて切り出して組み立ててみましょう。 11種類の 展開図パターン1つ1つには、回転させた状態と反転させたものがあり ます。 とはいえ、もとの形は1つ。 回転と反転のルールさえ分かってしまえば、あとは簡単です。 回転(かいてん)|90度 展開図パターン中3個の3番目を そして4週目である今週は、『サイコロ』でした。 サイコロは、立方体であると同時に向かい合う面の数字を合わせると7になるという特性があり、展開図にしたり積み重ねたり転がしたりとさまざまなパターンでの出題があります。 スポンサーリンク 予習した
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators筆記試験に出てくる展開図の問題は 「組み立てるとサイコロになるのはどれでしょう? 」 「☆印のある面と向かい合うのは、どの印の面でしょう? 」という感じです。 立方体が出来る展開図のパターンが頭に入っていて、どこの面が向き合うかが頭に 3つの基礎知識 基礎知識1サイコロは「対(つい)」で整理する 基礎知識2展開図には4つのパターンがある 基礎知識3展開図では、対になる面は「隣の隣」になる 例題でマスターしよう 例題1目の数の合計を求める 例題2ひとつだけ違う
サイコロ 展開図 パターンのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 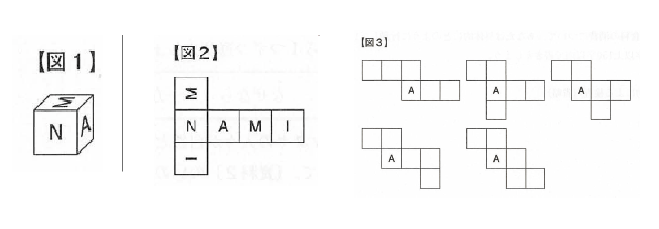 サイコロが最小の回転数で 全面回るパターンを考えてみた | 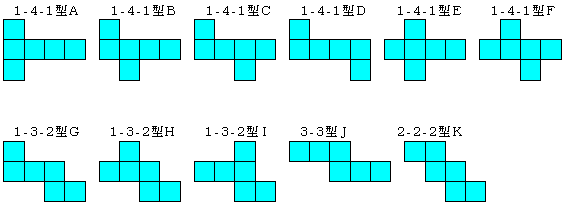 サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 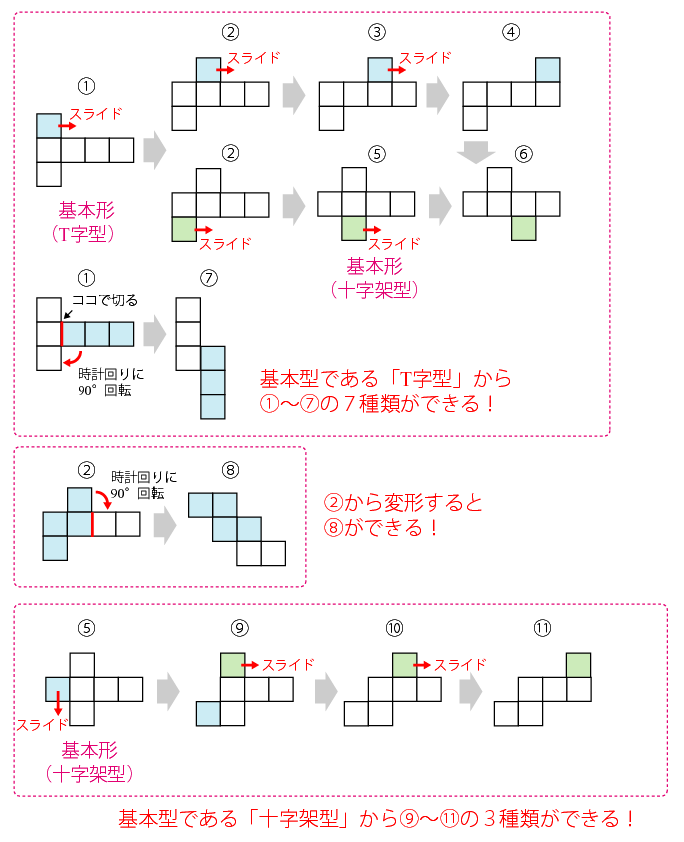 サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 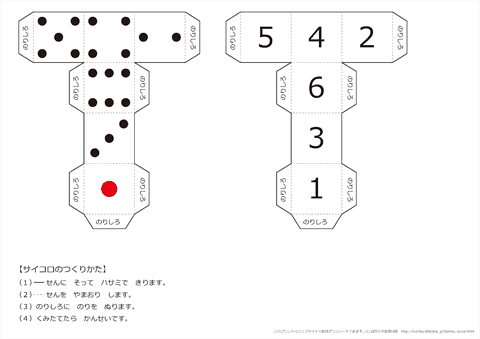 サイコロが最小の回転数で 全面回るパターンを考えてみた | 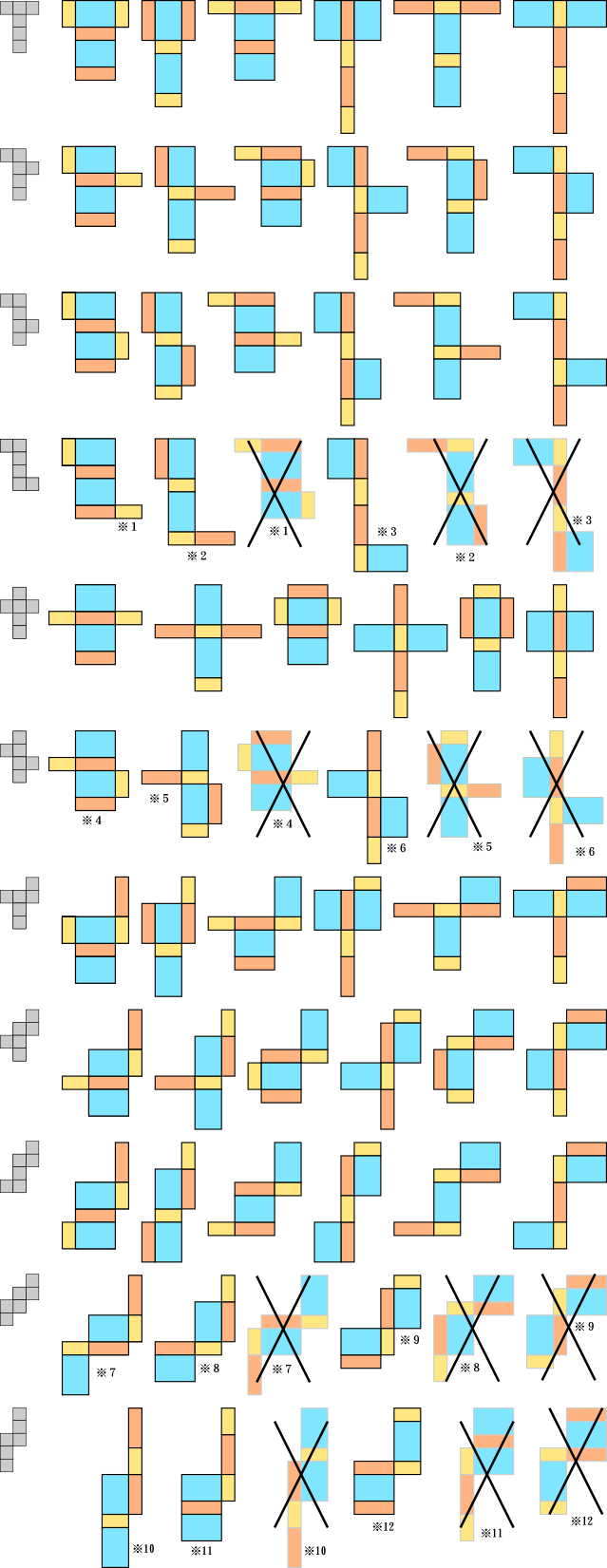 サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | 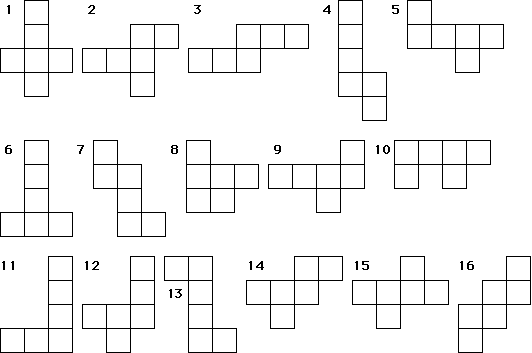 サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた | 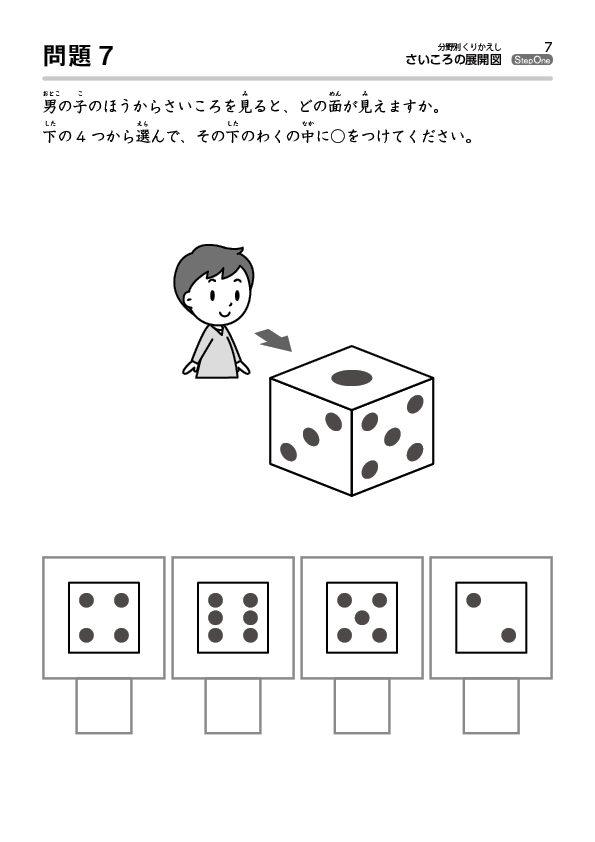 サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 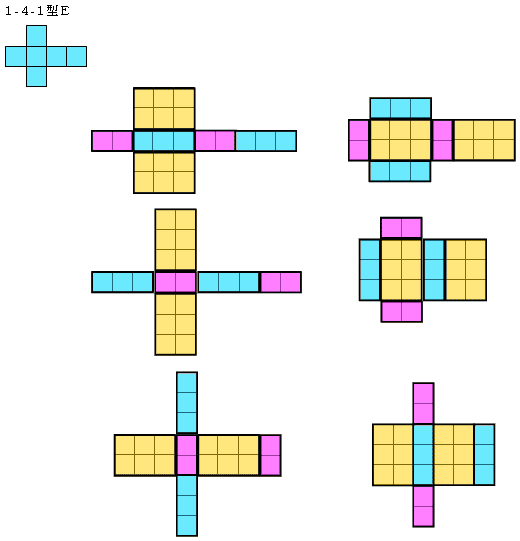 サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | 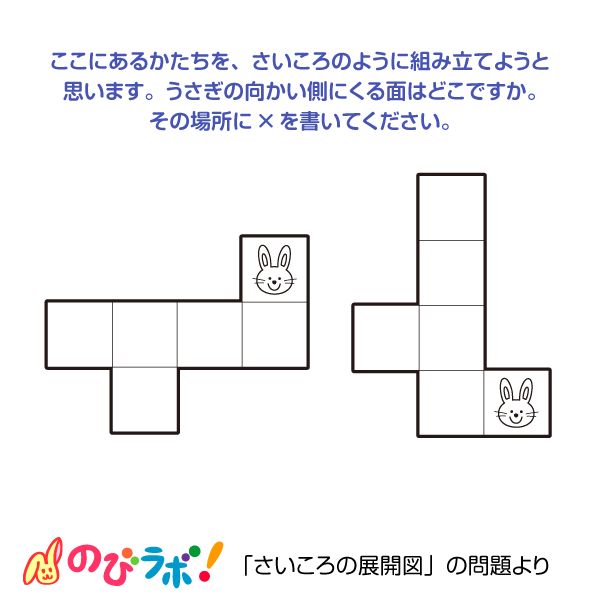 サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 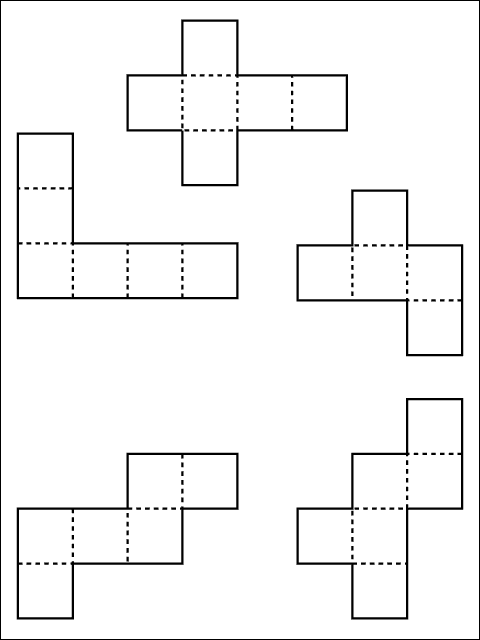 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
サイコロが最小の回転数で 全面回るパターンを考えてみた | 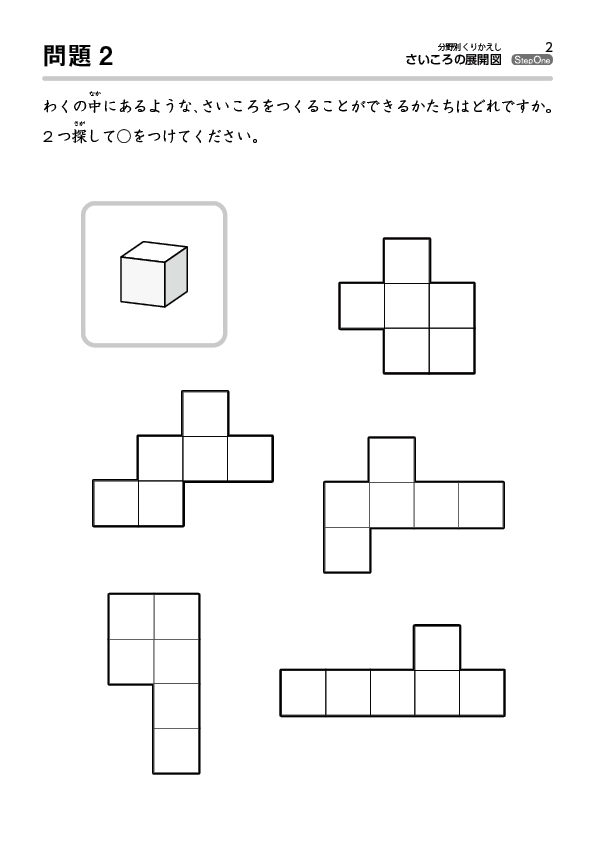 サイコロが最小の回転数で 全面回るパターンを考えてみた | 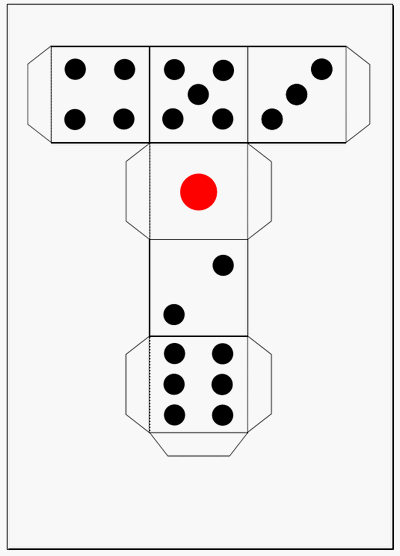 サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 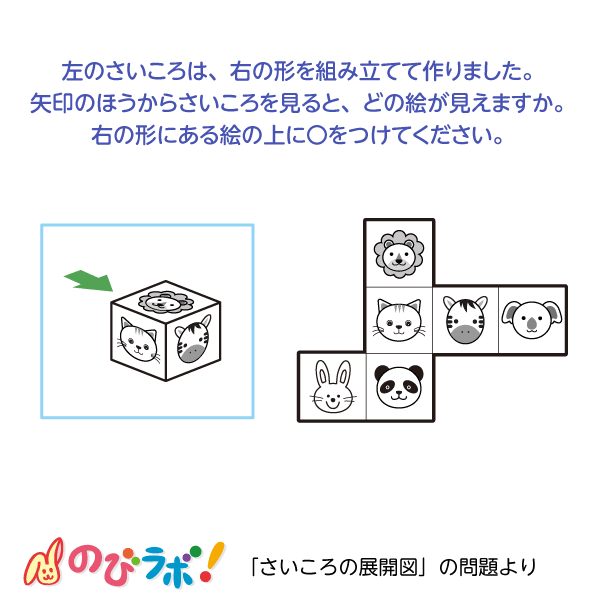 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 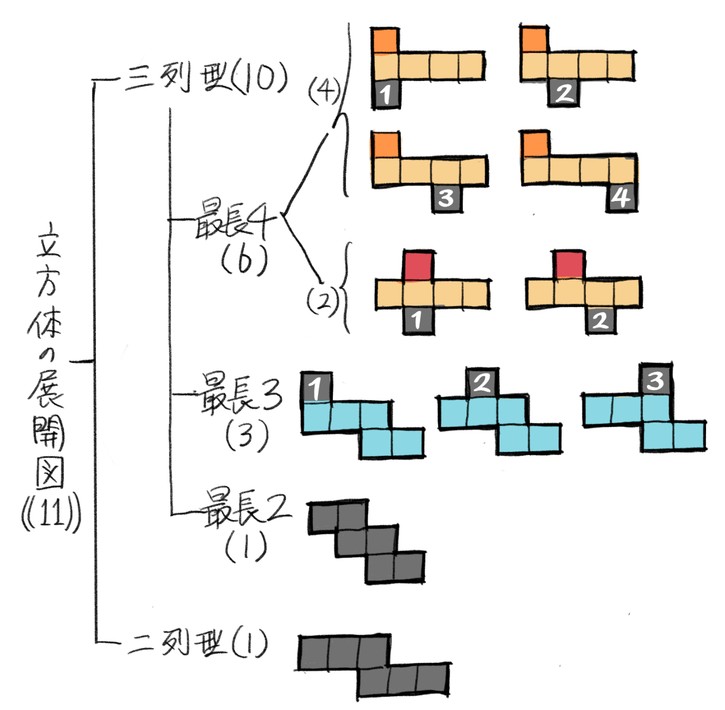 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 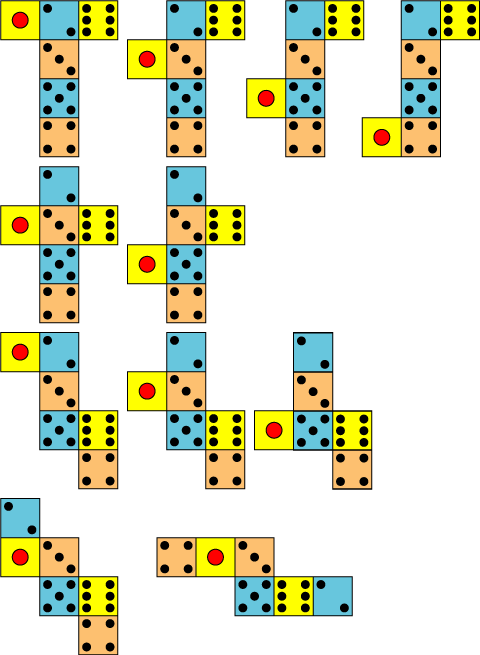 サイコロが最小の回転数で 全面回るパターンを考えてみた | 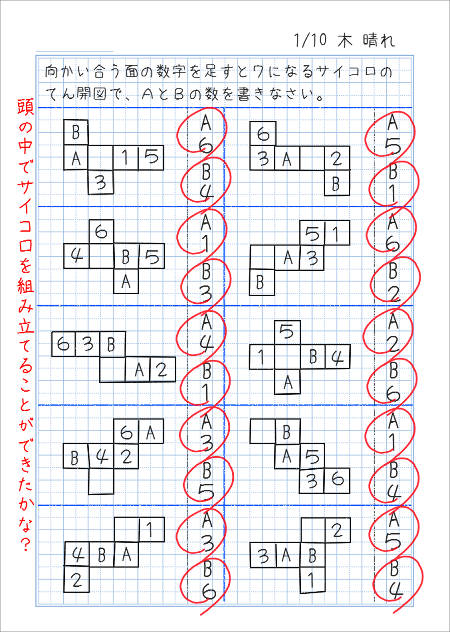 サイコロが最小の回転数で 全面回るパターンを考えてみた |
 サイコロが最小の回転数で 全面回るパターンを考えてみた | 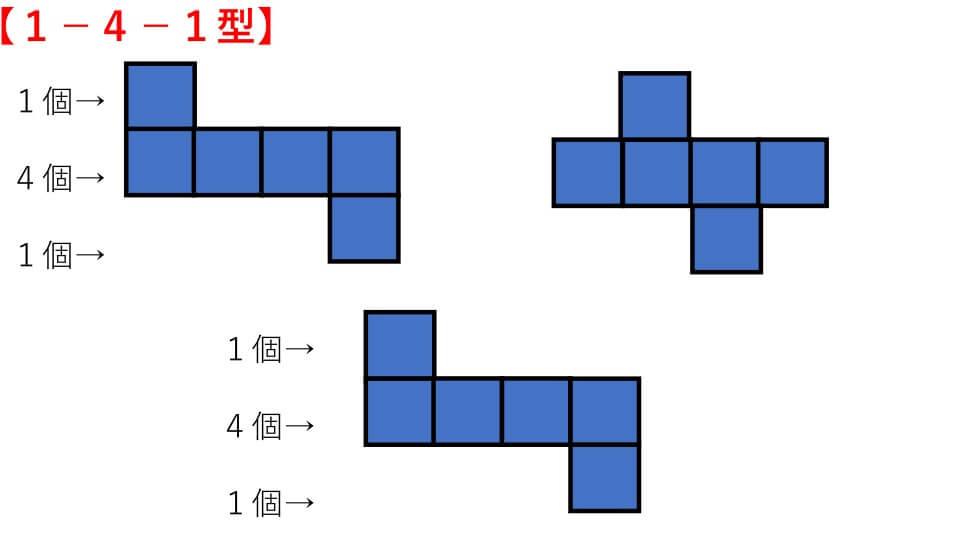 サイコロが最小の回転数で 全面回るパターンを考えてみた | 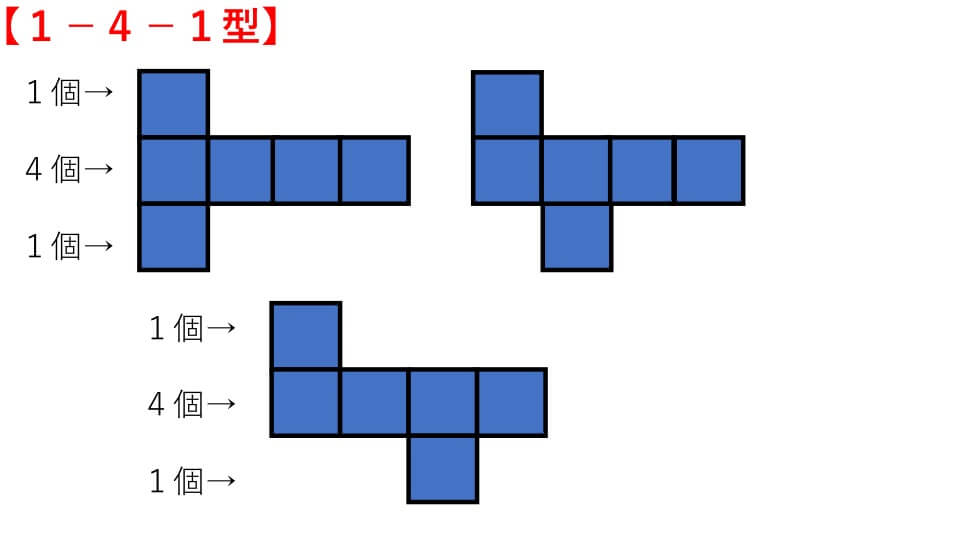 サイコロが最小の回転数で 全面回るパターンを考えてみた |
「サイコロ 展開図 パターン」の画像ギャラリー、詳細は各画像をクリックしてください。
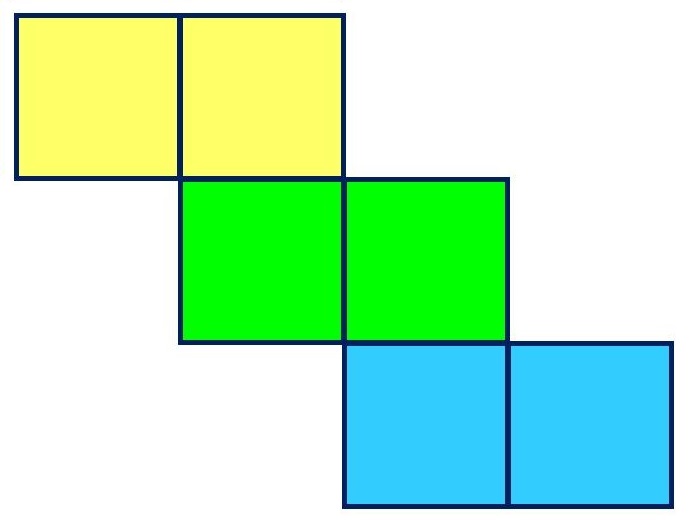 サイコロが最小の回転数で 全面回るパターンを考えてみた |  サイコロが最小の回転数で 全面回るパターンを考えてみた | サイコロが最小の回転数で 全面回るパターンを考えてみた |
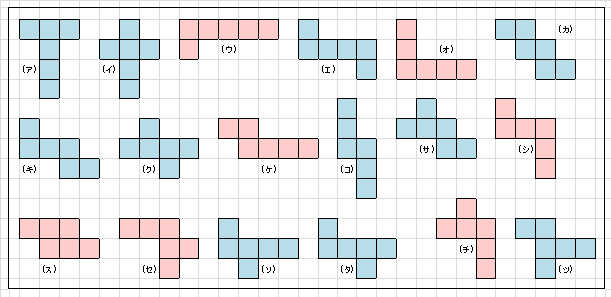 サイコロが最小の回転数で 全面回るパターンを考えてみた | 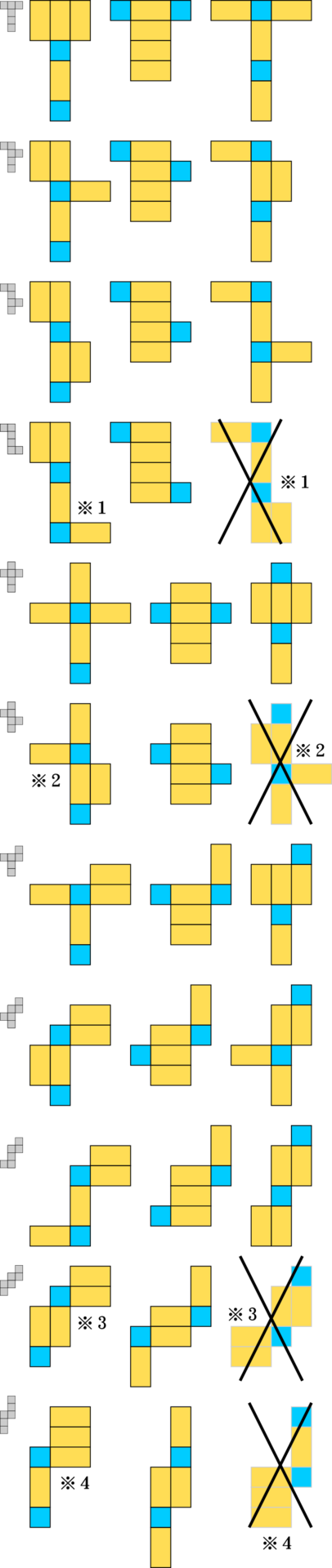 サイコロが最小の回転数で 全面回るパターンを考えてみた |
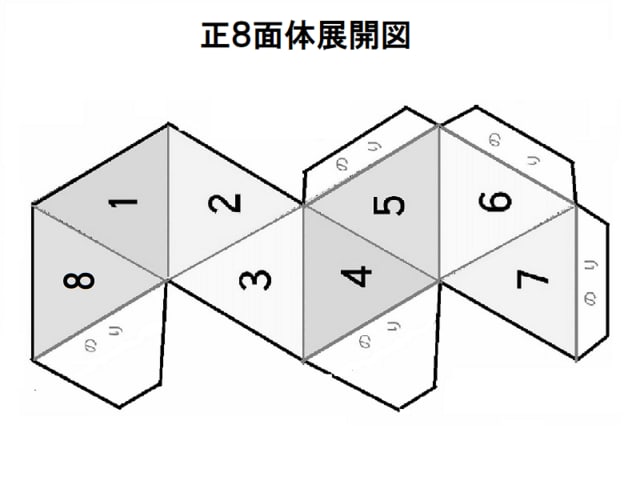
多面体サイコロ Polyhedral Dice 正多面体 正多面体(プラトンの多面体)は、全部で5つあります。 これらの展開図と組立図をご用意しました。 組立図をクリックすると、別ウィンドウで印刷用のpdfファイルが開きます。 展開図は321型となっています。これは先ほど説明した4パターンに当てはまっていません。ですので(例題1)の展開図を組み立てても 立方体にならないことがわかります 。 実際に書いてみたり、頭の中で組み立てて立方体をイメージする方法はありますが、パターンを覚えて考

コメント
コメントを投稿